Datos
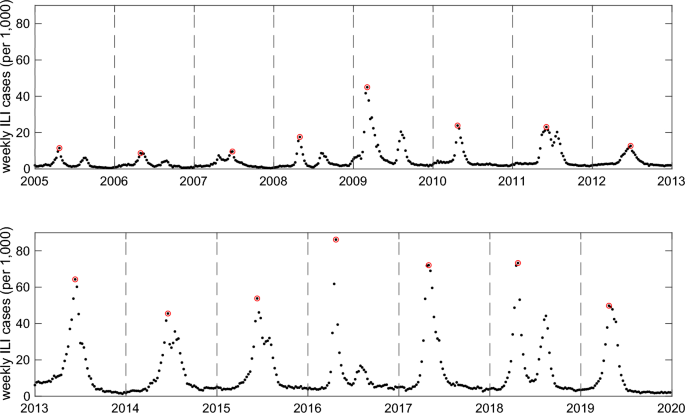
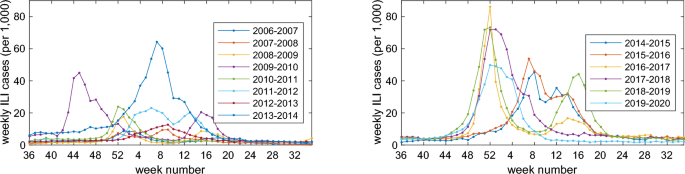
Para un pronóstico eficaz de la influenza, utilizamos los datos que se pueden recopilar de manera oportuna. La Agencia de Prevención y Management de Enfermedades de Corea (KDCA) opera un sistema de monitoreo de influenza durante todo el año, de septiembre a agosto del año siguiente, en anticipación a la epidemia invernal. Se trata de una crimson de clínicas ambulatorias, que informan semanalmente el número de pacientes que han tratado por enfermedades similares a la influenza (ILI). La tasa de consultas semanales por ILI en Corea, definida como el número de visitas de pacientes por enfermedades similares a la influenza por cada 1000 visitas de pacientes ambulatorios, se muestra en las Figs. 1 y 2. Aunque las tendencias temporales de la incidencia de ILI de 2005 a 2020 revelan un patrón consistente de propagación de invierno a primavera, el momento del inicio de la temporada y el pico epidémico anual varían según los años. Para estimar el inicio y el momento pico de la epidemia, utilizamos los datos semanales de ILI disponibles en el sitio net de la Agencia de Prevención y Management de Enfermedades de Corea (KDCA).31,32.
Casos semanales de ILI por cada 1000 pacientes ambulatorios en Corea del Sur desde la semana 36 de cada año hasta la semana 35 del año siguiente, cubriendo el período de 2005 a 2020.
Casos semanales de ILI por cada 1000 pacientes ambulatorios en Corea del Sur desde la semana 36 de cada año hasta la semana 35 del año siguiente, cubriendo el período de 2005 a 2020.
Paso 1: Detección del inicio de la temporada
Como paso preliminar en nuestra predicción de la hora punta, determinamos el inicio del brote estacional cada año. Para el análisis comparativo de la precisión de la predicción de la hora punta utilizando diferentes métodos en la detección del inicio de la temporada, presentamos tres formas diferentes de detectar el inicio de la temporada, a saber, conmutación de Markov, detección basada en umbrales y detección de hora fija.
-
Detección de tiempo fijo En el enfoque de detección, seguimos la convención de utilizar el 1 de octubre (semana 40) como fecha de inicio de cada año.
-
Detección basada en umbrales Aunque investigaciones anteriores han utilizado enfoques basados en umbrales para estimar el momento de inicio de la temporada de gripe, no existe un método estándar para establecer el umbral. En este estudio, el tiempo de inicio se outline como la primera semana en la que la tasa de ILI excede un cierto valor umbral.
-
Conmutación de Markov En ref.30, Los modelos ocultos de Markov se utilizan para distinguir entre fases epidémicas y no epidémicas. Adoptamos este enfoque para identificar el inicio de la temporada, que definimos como la primera semana de cambio de régimen de no epidémico a epidémico, comenzando desde el comienzo de la temporada de influenza en un año determinado.
Para (i en {1,ldots ,52}) y (j en {1,ldots ,15 })definimos (Y_{i,j}) como la diferencia observada de las tasas de ILI entre semanas (yo+1) y semana i en el año jy (Z_{i,j}) como una variable aleatoria no observada que indica la fase del sistema: 1 para epidémica y 0 para no epidémica. Para inferir el estado inobservable (Z_{i,j}) usando los datos observados (Y_{i,j})consideramos una cadena de Markov de dos estados de orden 1 con las probabilidades de transición definidas de la siguiente manera: (ok,l en {0,1}), (P_{ok,l}=P(Z_{i+1,j}=l|Z_{i,j}=ok),) dónde (P_{ok,0}+P_{ok,1}=1). La distribución condicional de (Y_{i,j}) se determina en función de si el sistema se encuentra en una fase epidémica o no epidémica, teniendo en cuenta que las dinámicas no epidémicas suelen presentar pequeñas fluctuaciones aleatorias alrededor de cero, mientras que las dinámicas epidémicas se caracterizan por cambios más grandes y más correlacionados.30. Modelamos la distribución condicional de (Y_{i,j}) como sigue: para (i en {2,ldots ,52}) y (j en {1,ldots ,15 }),
$$ start{aligned} & Y_{{1,j}} |(Z_{{1,j}} = 0)sim N(0,sigma _{{0,j}}^{2} ) , & Y_{{1,j}} |(Z_{{1,j}} = 1)sim N(0,sigma _{{1,j}}^{2} ), & Y_{{i,j}} |(Z_{{i,j}} = 0)sim N(0,sigma _{{0,j}}^{2} ), & Y_{{i ,j}} |(Z_{{i,j}} = 1)sim N(rho Y_{{i – 1,j}} ,sigma _{{1,j}}^{2} ), finish{alineado} $$
dónde norte denota una distribución regular. Tenga en cuenta que sólo necesitamos estimar (rho ), (P_{0,0}), (P_{1,1}) y ({{sigma ^2_{0,j}, sigma ^2_{1,j}: j = 1,cdots ,15}}). Para estimar los parámetros del modelo empleamos el método bayesiano con distribuciones previas.
$$ rho sim U( – 1,1),quad P_{{0,0}} sim B(0.5,0.5),quad P_{{1,1}} sim B(0.5,0.5 ). $$
aquí, Ud. denota una distribución uniforme y B denota una distribución Beta. Además, considerando que (sigma ^2_{0,j}) debe ser inferior a (sigma ^2_{1,j}) Debido a que sólo refleja variaciones aleatorias en lugar de los efectos de una epidemia, expresamos nuestro conocimiento previo sobre ({{sigma ^2_{0,j}, sigma ^2_{1,j}: j = 1,ldots , 15}}) a través de la siguiente estructura jerárquica:
$$ sigma _{{0,j}} sim U(theta _{{low}} ,theta _{{mid1}} ),quad sigma _{{1,j}} sim U (theta _{{mid2}} ,theta _{{sup }} ), $$
dónde (theta _{bajo} sim U(a,b)), (theta _{mid1} sim U(theta _{low},b)), (theta _{mid2} sim U(theta _{mid1},b)), (theta _{sup} sim U(theta _{mid2},b)) con números dados (a=0.1) y (b=20).
JAGS (Simply One other Gibbs Sampler) se utiliza para la estimación de parámetros y la inferencia de los estados ocultos. (Z_{i,j}). Tenga en cuenta que solo utilizamos partes de los datos de ILI (2005-2013) para la estimación de parámetros, dejando las partes posteriores (2014-2020) para fines de prueba. Los parámetros estimados del modelo de conmutación de Markov se presentan en la tabla complementaria. T1.
Finalmente, la probabilidad posterior de que una semana determinada esté en fase epidémica se determina tomando el promedio de las muestras de estados epidémicos. (Z_{i,j}) de esa semana. Si la probabilidad posterior es superior a 0,5, entonces la semana se clasifica como la semana en la fase epidémica. De lo contrario, se clasifica como fase no epidémica. Definimos el inicio de la temporada como la primera semana que se identifica como en la fase epidémica a partir de la semana 36 de ese año. Consulte la figura complementaria. T1 para la comparación de la curva epidémica de ILI y las probabilidades posteriores de la fase epidémica.
Paso 2: Predicción de los picos de brotes
Para estimar el pico de una determinada temporada de influenza, ingresamos datos semanales de ILI en el modelo SIR, comenzando desde la semana estimada del inicio de la temporada. La razón detrás de este enfoque es que las curvas epidémicas tienden a exhibir un crecimiento exponencial en la fase inicial, y el inicio de la temporada previamente estimado proporciona una estimación de cuándo comienza la fase de crecimiento exponencial. Al comparar la curva de ILI a partir del inicio de la temporada con la curva de infección del modelo SIR, podemos parametrizar el modelo SIR y obtener un pico de la temporada simulado por el modelo.
El modelo SIR describe la dinámica de Vulnerable (S), Infeccioso (I) y recuperado (R) población con las siguientes ecuaciones:
$$ frac{{dS}}{{dt}} = – beta Sfrac{I}{N},quad frac{{dI}}{{dt}} = beta Sfrac{I }{N} – sigma I,quad frac{{dR}}{{dt}} = sigma I, $$
dónde (N = S
